Square root on chip

Introduction

Wow, this is the first actual scientific post I think. This is a rare one, so let’s strap in. Square root. Pick a number. Now find 2 numbers that you need to multiply to get your targeted number. How do we find those 2 numbers? There are a couple of ways. In my work we will examine the iterative approach which takes us N cycles, where N is the number of bits of our square-root number. In this project we will be taking a look how we can process the square root of a number in digital logic, without any need for more complex calculations rather than simple bit shifts and a few adds or subtractions. When we are done with clearing up how our square root works we can program it onto an FPGA and when we conclude that that works we can move it to software for actual chip design.

Digital logic design

The whole thing may seem very complex at first, but there are a few things we must establish before we begin attacking this task, first as input we have a 24 bit number and as output we have a 12 bit number

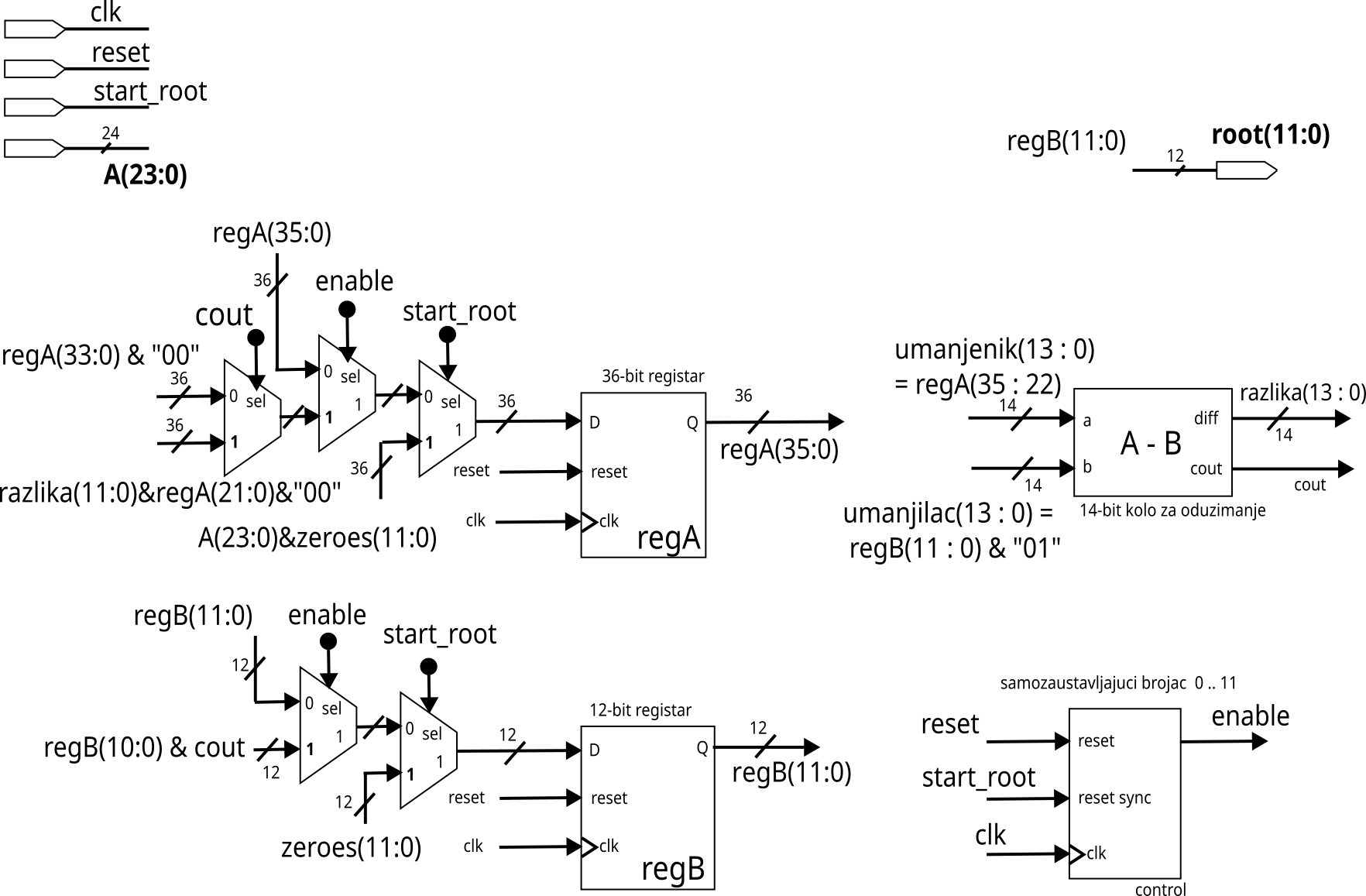
As shown on the diagram we have a couple of components to work with, a counter, 2 registers and a subtractor.

---

To begin executing the algorithm we first need to expand Register A by N/2, in this case 12 bits and reset our clock counter to 0, so that we can properly extract bits. In every iteration we extract 14 MSB bits of the register A and place them in the 14 bits of the Minuend, and to construct the subtrahend we need to take 12 bits of the register B and append “01” to them. Thus we have constructed our minuend and subtrahend, if their difference is negative, register A moves 2 bit places to the left while register B moves 1 bit place and the last bit is set to “0”. If the difference is positive register A gets a new value, 12 LSB bits of the difference, 22 LSB bits of register A and “00” at the end, while register B moves 1 place to the left and in the LSB place “1” gets written. We do this for 12 cycles until we reach the end_root signal.

---

Now that we are able to complete this task using digital logic, we can proceed to some more sophisticated tools.

C and assembly

To move our square root from an ASIC component to something more suitable for a micro controller we first need to see what happens in our code in a higher level language

uint16_t rootf(uint16_t input) {
    uint16_t accumulator = 0;
    uint16_t extracted = 0;
    int16_t bitDepth =7;
    
    while (bitDepth >= 0) {
        //extract bits
        extracted = (extracted << 2) | ((input >> (bitDepth * 2)) & 0b011);
        //subtrahend
        uint16_t sub = (accumulator << 2) | 1;
        
        if (extracted >= sub) {
            extracted -= sub;
            accumulator = (accumulator << 1) | 1;
        } else {
            accumulator <<= 1;
        }
        
        bitDepth--;
    }
    
    return accumulator;
}

This code doesn’t seem that complicated apart from the fact we do some dubious bitwise operations in order to extract the bits we need for every stage of the operation, in this particular example we used a 16 bit input just because it was easier to work with.

Now that we have this C code, we can compile it into something that is more in line with our own microcontroller architecture, it has a similar ISA as the PIC microcontroller, apart from the fact we cannot multiply or divide…

Writing the whole ROM file here would clutter the post so it is all available on my github.

Chip

The actual chip looks like this

There is not much I can say about it since I do not really know if I am able to provide any information without breaking any rules of my university but I am open to discuss things in private.

Conclusion

It is quite magical how we humans made tiny little sand pieces stand 20 nanometers apart from each other and then made them think. What human can tell you what is the square root of 34 in about 12 clock cycles * operating frequency( should be able to handle about 10Mhz). And the little rocks do it. Insanity. I wanna make my own chip one day. It’s gonna be a great journey.

There is room for improvement in this work, for example the precision could be improved since the output currently is only integers, if we could somehow get some decimals in there we could drastically decrease the error rate for small numbers while not taking too many more clock cycles, at most 2N